Consider these 3 hands. In all cases, you are not-vulnerable and the auction starts with 2 passes. Your methods are a strong 1♣ (16+, almost any distribution), 15-17 1NT, 5 card majors and a nebelous 1♦. The latter bids in the 10-15 range and your card says “light opening bids”. Your bid?
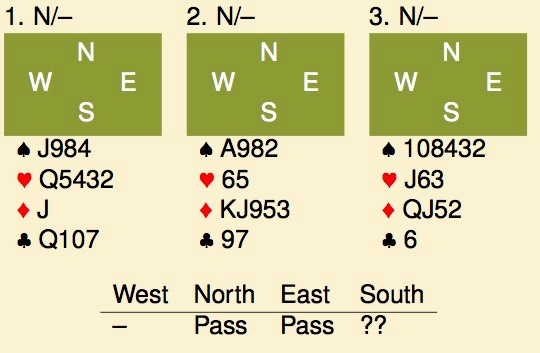
Well, you may not expect this, at least I’d pass most or all of them without the blink of an eye, but these hands were all opened when they were played at a recent world championship, with 1♥, 1♦ and 1♠ respectively. I can sort-of understand the 1♦ opener on number 2 if that would promise a suit, but it doesn’t. The two others look like downright psyches to me.
What is more surprising, is that these hands were all opened by the same US pair of Bathurst and Lall. After the third hand came up in the playoff match between Spain and the USA, the Spanish player noticed something odd. As far as he could remember, the US pair never seemed to pass in 3rd seat, not-vulnerable, when the auction started with 2 passes. That appears to be an undisclosed agreement.
Spain still had to play 32 of the 96 boards of the match and reported the matter to the TD. The TD didn’t take action other than that he’d said that the matter would be investigated later. A lot can be said about the way the Spanish complaint was handled, but that is not the scope of the article. If you want to know more details, go to bridgewinners.com and read what the Spanish captain and the US players (in particular teammates Hampson and Platnik) have to say about all this.
What I want to discuss here are the hands themselves. A couple of things can be the case here:
- Bathurst and Lall indeed have an undisclosed agreement to always open not-vulnerable in 3rd seat, even if they do not have opening strength (that is, 10+ points in their methods).
- All 3 hands were psyches (or systematic light openings, or systematics sub-standard opening bids, ot whatever you want to call them) and it just happened that 3 of them occured in a row.
The consequence of (1) is that all hands with 0-9 points have to be opened. That has 2 implications: first, this implies an agreement to open hands with 0-7 points at the one level and such method is a HUM (Highly Unusual Method). The use of HUM’s is restricted and was not allowed at this stage of the event. A second implication is that the convention card explicitly has to list this option. “Light openings, 10-15” is not enough, I think it should be far more explicit, I can see nothing wrong with “10-15 in 1st/2nd/4th seat, 8-15 in 3rd”.
Psyches are, of course, part of the game. A psyche is defined as an intentional and gross misrepresentation of your hand with the goal of confusing both partner and the opponents. Opening a 4 count certainly meets that requirement. But: part of a psyche is that is should be surprise to both the opponents and your partner. This is the tricky part, if you frequently psyche in certain situations, partner will notice a pattern and adjust his bidding accordingly. At that point, it becomes an agreement and this is subject to system restrictions and must be disclosed.
So, were these hands random psyches or does this pair have an unclosed agreement? Is 3 psyches in the 200 boards this pair played enough to make this an agreement. Is 200 boards enough statistics to make this judgement call?
To start with the last question. Ideally one would like to go to some kind of database and query it for all hands played at every event over the last years. Unfortunately, no such thing exists. We do have BBO achives though, and I had a bit of time, so I went through the vuegraph archives and found 3 more sets of boards which seem relevant:
- 2016 Vanderbilt: 5 session, 75 boards.
- 2016 USBF Trials: 19 sessions, 285 boards.
- 2016 Spingold: 6 sessions, 90 boards
- 2016 Wroclaw: 13 sessions, 208 boards
Or in total 658 boards. That is a bit more data. I’ve intentionally not included hands from tourmaments in 2015 and before, as methods and style may vary over time.
The next question is how many light openings did we see in this sample. At the same time, a property of a psyche is that they are random, i.e. sometimes one bids, sometimes one doesn’t. Thus, in these hands, one should also find hands where the player in 3rd seat passed. Going through the hands, we find:
- 2016 Vanderbilt: 0 light opener in 3rd seat, 0 3rd seat passes.
- 2016 USBF Trials: 0 light openers in 3rd seat, 0 3rd hand passes.
- 2016 Spingold: 2 light openers, 0 3rd hand passes.
 Boards are on the right, both from the round of 16.
Boards are on the right, both from the round of 16. - 2016 Wroclaw: 3 light openers, 0 3rd hand passes (see hands above).
In other words, in 5 cases out of 658 boards, there was a light 3rd seat opener, in none of the cases, there was a 3rd seat pass. I also found 3 13-point balanced hands upgraded to a 15-17 1NT, but that is also outside the scope of this article.
In case you wondered. One expects to find on average about 4 to 5 hands in a 650 board sample, where the auction starts with 2 passes, a pair is dealer and not-vulnerable. This depends a bit on how agressive one is with opening bids and preempts.
So, is there anything we can conclude from this?
On bridgewinners.com, one of the first comments was that there was not enough statistics to draw any conclusions. Is this really the case?
No, what we can use here are forensic statistics. This is a field of statistics where one tries to say something about probabilities based on limited data-sets without the possibility to do more experiments in order to collect data.
In forensic statistics, it is common to look at the statistical value of a piece of evidence. Simply put, this is a way to quantify the value of a piece of evidence in support of one of two hypotheses. The hypotheses are usually that X did something (illegal and X is thus guilty of some crime), or that somebody else did the same thing (and thus X is not guilty of the crime). The number is defined as P(E|H1)/P(E|H2}, or the ratio of the probabilties that the evidence would show up if hypothesis H1 or H2 was true. If the ratio is 1, the evidence equally supports either hypothesis, if it is larger than 1 it supports H1, if it is smaller than 1, it supports H2. Note that this does not say that either hypothesis is actually true, to calculate that one needs the ratio P(H1)/P(H2), or the probabilty that either hypothesis is true in absence of any evidence, as well.
I’ve now tried to summarize about 500 pages of complex statistical theory into a single paragraph and if you have never studied this, it might not be very clear. However, this is considered the best current practice of using the data amongst statisticians worldwide.
Let me give you an example: John is found shot dead in his home. One possible explanation is that his wife Myrtle shot him (hypothesis H1), another one is obviously that somebody else did it (and thus Myrtle didn’t, hypothesis H2). The police investigates and finds a neighbor saying that John and Myrtle had a fight over a bridge hand the day before the murder. That might be a motive and thus increases the possibility that Myrtle shot him over the theory that somebody else did this. The value of this evidence is thus larger than 1, say 2. On the other hand, another witness says that Myrtle was in Amsterdam on the evening that John was shot in London. She could have returned, shot him and flown back, but that is very unlikely and the value of this evidence would be (say) 0.001, strongly supporting the theory that Myrtle didn’t do this. It should be noted that all that this does say, is that both pieces of evidence support a hypothesis, and that the second one is more important than the first one. However, it does not say that Myrtle did or didn't do this, it just makes it more or less likely and it gives a objective way to compare the two statements.
OK, so we have our 5 hands in a sample of 658. We have 2 hypotheses:
- H1: The pair Bathurst - Lall has an undisclosed agreement to always open in 3rd seat not vulnerable and never pass, even if that means bidding on less than opening values.
- H2: Like all bridgeplayers, these players occasionally psyche and it is just a coincidence that this happened 5 times in a row on these hands.
We have the evidence that on 5 hands, all 5 were opened. What is the value of this evidence?
For hypothesis H1, this is simple: the agreement is to open these hands, so they will be opened. P(E|H1) is thus 1.
For hypothesis 2, it is a bit more complicated as one has to estimate the probability that any bridge player will psyche in third seat with a suitable hand. However, one might also pass on those hands. Let’s first say that the decision to bid, is made by flipping a coin. That translates to an average 2.5 psyches over 650 boards. However, in this case, the probabilty that one psyches 5 times in a row on 5 boards, is still only 1/32 or about 3%. P(E|H2) then becomes 3% as well and the value of the evidence is 32.
To put the numbers into perspective, if one plays 2 club games a week, 2.5 psyche on average translates to 1 psyche a month and I hardly believe that most players psyche that often. At least, I don’t and I’d go nuts if my partner did this as frequent as this. If we reduce the frequency of psyches to 10%, or once about twice a year, the probability of 5 psyches on suitable hands in a row decreases to about 0.001%. The value of the evidence is then 100,000.
A value of 32 (or anything between 10 and 100) is considered to be somewhat supportive of H1 over H2, 100,000 is strong support for H1 over H2. Something in the middle supports H1 well over H2.
Of course, this is only one piece of evidence and that is by definition not sufficient to convict anybody of anything, so further study is needed. That could be more hands, but also a hearing of the players by their federation and/or the new high level players committee set up by the WBF, a study of their system notes and what not.
Conclusion: Reviewing 658 recorded hands played in the 6 months in or before Wroclaw, I found 5 out of 5 boards where this pair opened on sub-standard hands in third seat over none where they did not.
Applying standard forensic statistical theory, this increases the probabilty of an undisclosed method to always open these hands, over random psyches that just happened to occur, by a factor between 32 and 100,000. That strongly implies that the auctions of this pair need more review.
