Today’s problems, though some of you may have seen them on Facebook before:
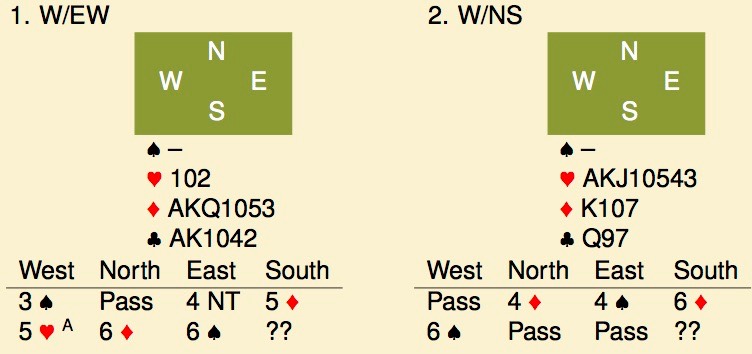
Butler scoring, decide on your action before reading on...
You have probably noticed something about the hands. In both cases, you have a spade void.
Something rare happened at the club this week: on two boards, both north and south had a spade void on the same hand, while EW divided the 13 spades amongst themselves. Needless to say, the results on those boards were rather wild. More about that later, in the post-mortom the discussion started with the obvious remark that people had never seen 2 voids in one suit on a single hand before and the question was raised how often this happens.
Estimates on facebook ranged from 50% (it happens or it doesn’t happen), via once every 200 years, to better buy a ticket in the State Lottery and hope for the jackpot. The latter, incidentally, happens once in about 2.7 million times.
Guesses aside, let’s just calculate this.
First the probabililty that one side holds 0 cards in spades: There are 52 cards in a deck, 13 spades and 39 others. When a deck is shuffled and dealt, both sides effectively randomly draw 26 out of the 52 cards. Combinatorics, the sub-field of mathematics that deals with this, will tell you that there are PN(n) = N!/(n!(N-n)!)) ways to do this. N! is shorthand for the product 1x2x3…N, with 0! = 1. In this case, N=52 and n=26, so P52(26) hands. If NS have no spades, they must select 26 cards out of the 39 non-spades, or P39(26), and select 0 cards out of the 13 spades, or P13(0). The latter is 1, as there is only 1 way to pick 0 cards out of 13: don’t touch any of them.
Divide the two and you have the fraction of hands with no spades for NS: P39(26)P13(0)//P52(26) = 39!/(26! 13!) . 13!/(13! 1!) . (26! 26!) / 52! = 39! 26! / 52! 13! = 1.64.10-5 or about 1 in 61000 hands. To put the number in perspective, if you play 100 boards a week (that is 4 club games), you play about 5200 boards a year.
Note that this is the specific case where NS hold 0 spades. The probability that either side has 0 spades, is twice as high as EW can hold 0 spades as well. The probability for this to occur in any suit is 4 times as high, making the probability for either side having no cards in any suit about 1 in 7500.
Now what about this coming up twice in a set of 28 boards? Let’s start with the 0 spades case. If the probability for something to occur in an experiment is X, and you repeat the expertiment N times, the probabilty that this will occur in n times, is: PN(n) . Xn . (1-X)(N-n) .
In our case, N=28, n=2, and X is 1.64.10-5. Substituting all this, we end up with a probabilty of 1.01.10-7, or 1 in about 10 million games, for NS not having any spades on 2 hands in a set of 28. Yes, you will win the state lottery more often. And for completeness, the probability that on 2 hands in a set, either side has no cards in a suit, is about 1 in 154,000.
Back to the hands:
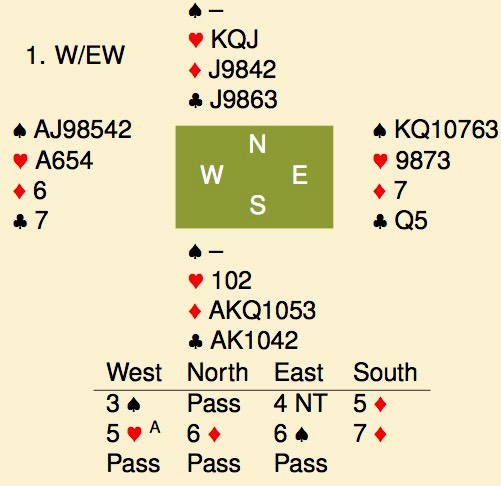
With these extreme distributions, one can try to be intelligent and say what should have been done but the fact of the matter is that it is usually your best guess, with little theory to support you. So, I’m just showing what happened at our table without too much text.
Sitting east, I could see that there must be 2 spade voids in the oppenent’s hand and thought to be clever by asking for aces to figure out if partner had a trick in a side suit. Added benefit is that, after 3♠-P, LHO must have a monster hand with a spade void. 4NT definitely will confuse him to some extend. Partner had an ace, so I stopped at 6♠ figuring it to go down about 3 against their slam. No plans to bid 7♠. South thought his spade void was worth something extra and bid on. Down 1, 13 imp’s away.
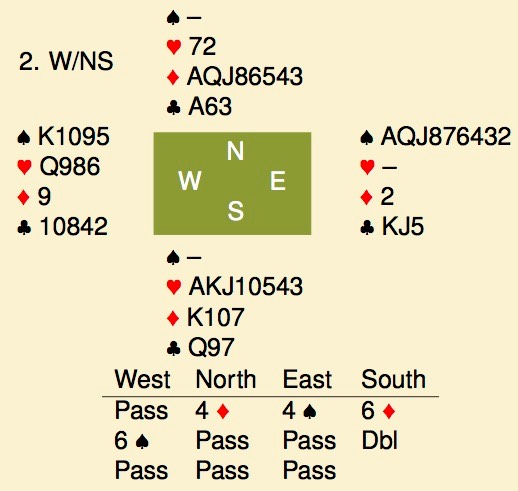
7♦ makes: ruff the ♠A opening lead, cash a high trump, play ♥AK and lead the ♥J. East covers but you ruff and have ample discards for the clubs. For this to work, partner needs the ♣A plus good diamonds and 1 or 2 hearts. Now, pass over 6♠ by south is presumably forcing, showing a first round spade control. After the previous board and with the calculation above, North couldn’t believe that they had 0 spades for the second time in the same session. That suggests a holding of ♠A(…) opposite a void, which is kind of useless. A third ace with south is clearly impossible, so north didn’t take the risk. 6♠x was about average.
Finally, a big thank you to all you readers. At the bottom of the pages, there is an ad placed by Google. If you click on the ad, you are redirected to the vendor and Google transfers a few cents into my account. Last month, for the first time in 7 years, the number of clicks was such that I made it above the threshold and got a payment from Google. So thank you, keep reading, and if you like the articles, click on the ad. It will help me to cover the cost of maintaining the site.
