The 1969 Bermuda Bowl was the first in history on a number of fronts. More about that later, first a bidding, lead and play problem.
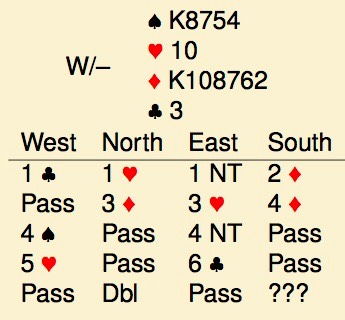
1♣ showed 16 or more points, any distribution, 1NT showed clubs and values for game, 3♥ a general force, 4♠ cuebid, 4NT asked for aces with 5♥ showing 2. So-far, so good, but your partnership has decided to play a new invention called the “sacrefice slam double”. If you have bid and raised a suit, and the opponents bid slam, a double shows 1 defensive trick asking you to pass if you have one too, or bid 6♦ if not. Your bid?

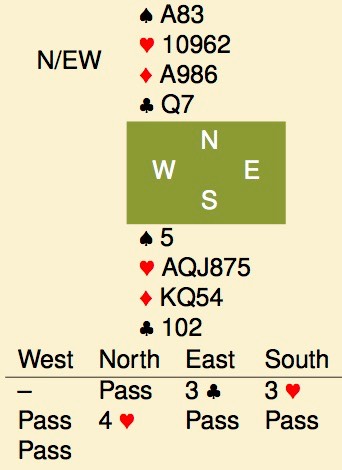
Same hand, different auction. 1NT 16-18, 3♣ natural, 3♥ natural and partner comes up with a Lightner double. Your lead?
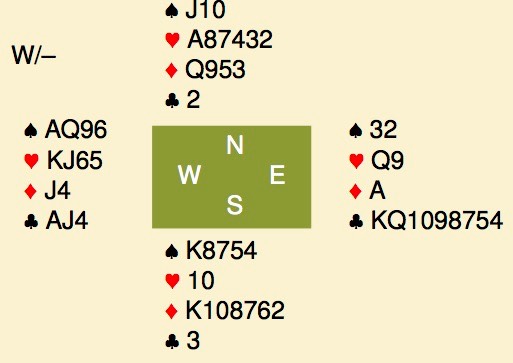
You are in 4♥. West leads the ♣K and switches to ♠7, in principle 4th best. Plan the play.
If you think that is too hard, here is a clue: You win, ruff a spade and return a club. East wins while west discards the ♠2, east plays another spade ruffed. Everybody follows to the ♥A. Time to claim the contract? If so, state your line of play.
While you are considering your actions, here is what was new at the 1969 Bermuda Bowl. First, it was the first year that professional teams came into play. In the Far East, the US-Chinese shipping magnate had devised the Precision system. He wanted to show that his system was better than anything else, so he hired a young Chinese (Formosa, or Nationalist China, or Taiwan as it is known today) and paid them to play. The team qualified as the representatives from the Far East.
In the US, Ira Corn had established the Dallas Aces, with the goal of bringing the Bermuda Bowl back to the US. However, qualifying rules being what they were back then, meant that that team could not enter yet and we’d have to wait until 1970 for their first appearance. Instead the US fielded a team selected through pairs trials. Pair trials have the intrinsic problem that, while you pick the 3 strongest pairs, you don’t necessarily pick the 3 pairs that function best as a team. The result confirm this. For the first time since the start of the Bermuda Bowl in 1951, the US team failed to qualify for the finals. Instead, the young Chinese team qualified finished second in the round robin and earned the right to play Italy.
All this didn’t bother the Italians too much. The team was at the top of its power, won the qualifying round robin and took on the Chinese. The first 2 sessions were more or less even (54-50), then the Italians turned on the afterburners: 70 imp’s ahead at the halfway point, 200 after 96 boards, eventually winning by some 250 imp’s after 128. That is more than 2 imp’s per board.
The final thing: after this final, and having won 10 Bermuda Bowls in a row, the Italian team announced their retirement from tournament bridge. At least for a couple of years, they’d be back.
The problems. What you don’t want, is to sacrefice against a slam only to find out that both you and your partner have a defensive trick. The Sacrifice Slam Double was invented to avoid that. The problem with this approach is, of course, to judge whether you will also take a trick against their slam. The French south didn’t and bid 6♦, for an obvious down 3. I tend to agree with him. The ♠K is definitely of limited value with the ♠A behind it, the _K is unlikely to produce a trick, and partner needs the ♥A and find the specific defence of ♥A, ♥-ruff to defeat the contract. Remember that west would be playing the final contract.
I have played SSD’s back in the 1980’s, but soon dropped them as it is one of those conventions that solves one problem and creates a new one like the one here. And, of course, even if you can show that you cannot defeat the contract, that doesn’t imply that you can take sufficient tricks for the save to be profitable.
In the replay, the double was Lightner, suggesting an unusual lead. That points towards hearts so south duly lead his singleton for down 1. Of course, this was fairly lucky, one can say that North doubled for his partner to have a singleton heart, as with 2 hearts the auction would have gone the same.
The ♣K lead and switch suggest that west had a singleton, and the suit is divided 8-2-2-1 around the table. A four-card major on the side of a preempt wasn’t done back then either, so we assume 3 spades with east and a 3-1-1-8 shape. West then has a 6-2-4-1 shape. Odds are that the ♥K is with west, that is (besides the ♣AK) a third loser. We thus need to tackle the diamonds for 0 losers, bearing in mind that the suit splits 4-1. ♦J or ♦10 singleton is an option, but that is fairly unlikely.
One way to get rid of the loser, is to eliminate the black suits and then put somebody on lead with the ♥K. So, win the ♥A, ruff a spade and play a club. East wins and must return a spade. Declarer ruffs, cashes the ♥A with both sides following. Another heart follows endplaying whoever has the ♥K.
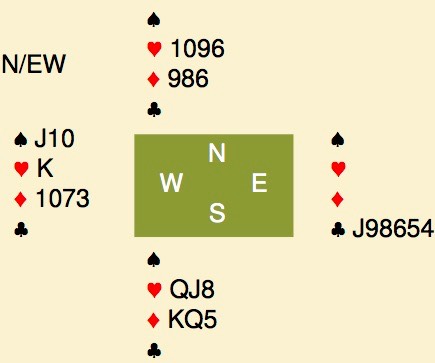
Note that his line of play also works when east has a 3-0-2-8 shape (declarer simply gives up 3 tricks), or when east has 3-2-0-8 with ♥Kx. He wins the ♥K and is forced to give up a trick with any black suit return.
Finally, it may appear that a diamond return in trick 5 would defeat the contract, but that is not true. Declarer plays small, west puts in the ♦J or ♦10. Now declarer, ruffs a spade and plays the ♥A and reaches this position. He plays a heart, west wins but is forced to lead away from ♦10xx.
